胡一天專欄：金融大海的數理波紋

在金融科技成為世人朗朗上口的名詞之前，金融界的「火箭科學家」們所關注的科技，是一系列被統稱為「數理金融」（quantitative finance）或「金融工程」（financial engineering）的應用學科集合。因為金融是在商業交易與市場習慣中形成的實務教訓與經驗法則，金融學家與金融工程師必須直面金融市場參與者每天面臨的實際問題，而不能純粹浸淫在由黑板上推導出來的方程式與抽象理論。金融市場每天開張，一秒鐘幾十億上下的各種交易態樣提供了豐富場域及巨量數據用以建立數理模型，驗證假設，執行實戰策略。這雖然讓金融較其他關注更形而上議題的社會科學更接近自然科學，然而金融市場瞬息萬變，眾多變數分分秒秒在影響金融市場。如此高度複雜的系統，既有一本萬利的誘人商機，又暗藏爾虞我詐的陰狠殺機。驚濤駭浪，淘盡古今多少豪傑。

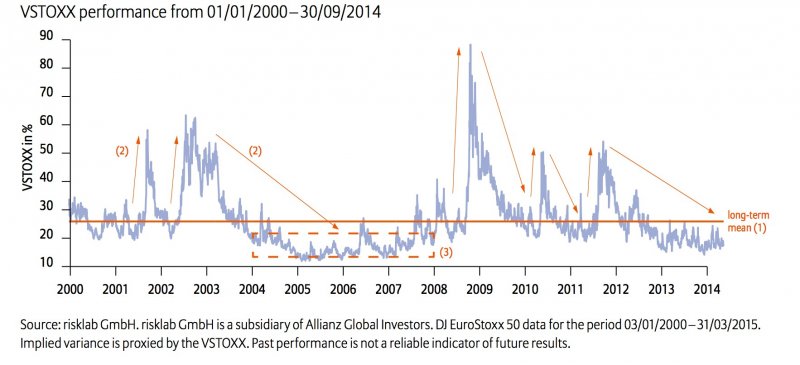
1827年，英國植物學家布朗在顯微鏡下觀察到水中的小花粉的隨機運動。後人將他發現的這種在自然存在的隨機運動稱為「布朗運動」(Brownian Motion)，並試圖對呈現布朗運動的自然現象建立數學與物理模型，探究規律。1905年，法國數學家Louis Bachelier 將有關布朗運動的知識用在研究巴黎股票市場上，並發表了一篇《投機理論》（Théorie de la spéculation）。在這篇被巴黎學術界認為太過前衛的論文中，Bachelier不但給出了布朗運動的數學模型，還率先將股市投資人和投機份子的每次交易，看成是如同遵循布朗運動的花粉隨機漫步，並得出了讓股市老師難堪的結論：股市投資高度隨機，後市難料，如果把時間軸拉長，股價的波動幅度將會擴大，波幅與時間跨度的平方根成正比。

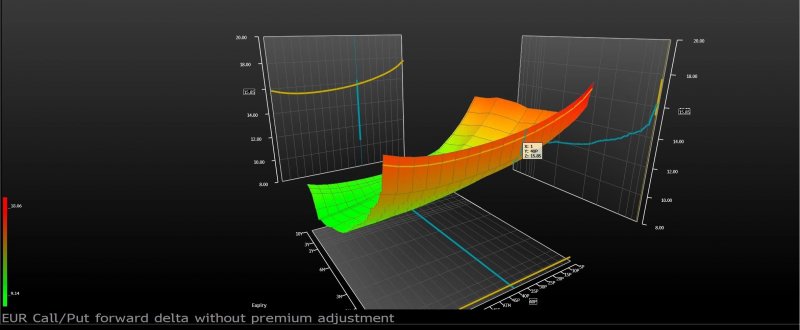
Bachelier企圖建立市價波動概率法則的嘗試是人類文明史上首度對金融市場進行數理模型建構，隨後開啟了1960年代時第一代金融工程理論的研發。獲頒1997年諾貝爾經濟學獎的Black-Scholes-Merton（BSM）定價模型以及當今全球交易量以兆美元計的金融衍生品市場的濫觴，都可溯源到Bachelier。因為Bachelier的理論模式是代數布朗運動，假設股價變化是常態分布過程，但股價不可能為負數，BSM模型將其修改成幾何布朗運動，假設股價變化的自然對數呈常態分布，這樣就可以套用物理學中的熱擴散方程，從而導出BSM無套利金融衍生品定價公式： （相關報導： 胡一天專欄：壟斷性行業的創新責任 ｜ 更多文章 ）

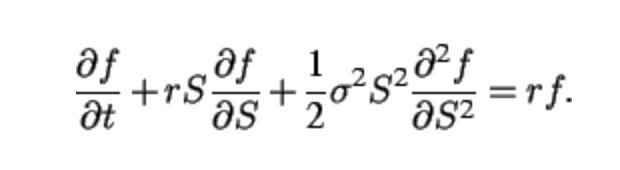
在這個隨機偏微分方程中，f是金融衍生品的價格，S是原生資產的市價，r是無風險利率，σ是原生資產市價的波幅。直觀來看，BSM公式假設金融衍生品（例如股票期權）的大盤商可以在微小的時間跨度中，透過買賣原生資產與以無風險利率拆借資金「合成」該衍生品。這個製造過程需要使用的「原料」（例如股票與債券）之間的「比例」（即所謂的對沖值 delta）可以用BSM公式推算出來。因為BSM模型假設股票走勢遵循幾何布朗運動，所以需要考慮修正項。這個修正項的來源，就是Bachelier指出的股價波幅正比於時間跨度平方根的關係。

假設r趨近於零，同時大盤商可以幾乎無摩擦力地買賣股票，上述公式等於在每一個微小的轉瞬之間，大盤商「生產」這檔期權做市的利潤趨近於零，前提是大盤商可以消除掉股價的一階影響，但無法消除掉二階影響。因此大盤商如果要從衍生品當中套利，必須要承擔波幅的變動風險。如果在到期日前在市場中量度到的實際股價波幅比當初在給期權定價時的隱含波幅低，相當于買入期權的投資人高估了股價變動的波幅，賣出期權的大盤商所賺取的利潤，正比於這兩種波幅的差額。這個推論的含義，是一個被消除了股價一階影響（即所謂的delta hedged）的「股票＋期權＋債券」的組合，可以視為針對股價波幅的預測值與實際值之間差距的賭局，勝負誰屬，交由時間判斷。

這個看似嚴謹的數理模型理論，其實隱藏了預測未來股價波幅的方法論與金融衍生品定價模型的本質問題。我在紐約曾師從過的Emanuel Derman，是世界知名的金融工程師，他最近將在紐約哥倫比亞大學講授金融衍生品與波幅建模的研究生講義結集，出版了一本新書《The Volatility Smile》，正好為這個本質問題的研究與實務上面臨的挑戰提供了一個豐富的階段性總結。

在1973年BSM模型被以正式學術論文的形式發表之前，股票與股市指數期權的交易已經發展了很多年。在那個沒有數理金融的蒙昧時期，期權大盤商的交易員在為不同到期日與不同履約價的期權定價時，多半依據經驗法則與實戰中培養出來的直覺。BSM模型的橫空出世，提供了切合交易實務需求的定價與報價機制，也催生了芝加哥期權交易所(CBOE)的創辦與勃興。因為BSM模型假設股價的波幅是一個常數，不同的股票因為其風險不同，會有不同的波幅。從BSM模型的角度來看，理論上一檔股票只會有一種波幅。這個波幅若當成是BSM的輸入，在給定其他變量的前提之下，可以算出某檔期權的在當下的理論價值。反之，若將某檔期權的市價視為輸入，在給定其他變量的前提之下，可以用BSM公式逆推出一個可以讓理論值符合市價的「隱含」波幅。理論上，隱含波幅是從包含了市場對該檔股票未來走勢的預期的期權價格中推算出來的預測，因此也就可以視為對股價在該檔期權到期日前波幅的估計，不會受到履約價的影響。在1987年紐約「黑色星期一」股災之前，這個假設與實證上觀測到的數據相符（下左圖），但在1987年大崩盤之後，履約價離現貨價愈遠的期權隱含波幅，反而愈高（下右圖）。 （相關報導： 胡一天專欄：壟斷性行業的創新責任 ｜ 更多文章 ）

從市場集體心理面來看，由於1987年黑色星期一時美股標普指數全日暴跌近23%，是一個統計上的極端黑天鵝事件。股災之前，市場參與者往往認為這種極端事件只是理論上參考，在股災之後可能開始認識到投保巨災險的必要，增加的需求導致華爾街生產與對沖價外期權的潛在賠付金額增加，因此導致一檔股票用BSM公式在不同履約價上逆推出來的波幅不同。這個被稱為「隱含波幅微笑」（volatility smile）的現象，顯示了全球金融衍生品的交易與風險管理的基礎模型有缺陷。如何彌補這個缺陷，就成了金融工程產業的核心增長動力，也是全球金融市場內秉的系統性風險關鍵指標之一。

金融工程的祖師爺Fisher Black（即BSM中的B）曾說：如果一個模型有缺陷，不一定是模型出問題，往往是我們對事物的認識與理解有問題。基於模型缺陷的隱含波幅微笑之所以成為金融工程產業增長的原動力，是因為很多第一代的金融工程師與在市場中實際參與交易及風險控管決策的專業人士，多半都抱持著一種迷思：如果既有的模型有缺陷，那就發明更能符合實證結果的模型。於是乎各類BSM模型的延伸紛紛出籠，用的數學愈來愈複雜，除了降低各種理工背景的火箭科學家在華爾街的失業率之外，對理解金融市場的本質不見得有幫助。直到2008年全球金融海嘯，人們才又一次學到了昂貴慘痛的教訓。監管確實變嚴格了，但各種炫技的數理模型依然持續在論文中出現，相關的新金融商品也不斷被華爾街金融化工廠合成出來向全球販賣，隱含波幅微笑曲面，依然存在。市場究竟需要新理論，還是新思維？這是一個trillion dollar question。

若暫時忽略金融工程本質的哲學思辨，隱含波動率微笑曲面亦提供了創造新金融商品的機會。既然隱含波幅是對未來實現的波幅的估計，華爾街就援引遠期利率是近期利率的估計這個例子，設計了一個「方差掉期互換合約」（variance swap，方差是波幅的平方，在數學上處理起來比較方便）。簡單地說，對某檔股票或股市指數未來隱含波幅看漲，可以用方差互換合約與華爾街大盤商針對未來不確定會如何浮動的隱含波幅對賭。這個賭局的累積賺賠，與前述delta hedged對沖組合相仿，可以寫成下列積分式：

這個公式中兩種波幅的差額對股價的走勢有路徑依賴性，必須消去股價的二階影響，才能製造一個針對波幅的純粹賭局，才能更精準地對沖風險。要完全消除股價的二階影響，理論上需要一個「對數合約」-- 到期日支付股價的自然對數值的合約（因為自然對數微分兩次後會抵銷掉積分號中的股價平方項），實務上這個合約不存在，但可以用一系列歐式期權的組合來逼近對數合約的理論值。這其實正是方差互換掉期合約的風險管理核心命題，也是全球金融市場高度關注的隱含波幅指數VIX及其衍生工具的理論基礎。 （相關報導： 胡一天專欄：壟斷性行業的創新責任 ｜ 更多文章 ）

近年來許多宏觀策略對沖基金也將隱含波幅/方差的估計與風險控制列為量化交易操盤的一大重點。假設隱含波幅有一個穩定的長期平均值，且在每次偏離其平均值後都會有向該平均值回歸的趨勢，只要能夠針對這些統計特性建立禁得起壓力測試考驗的模型，無論是波段操作，或是把操盤的基金當成再保險公司，透過承擔黑天鵝風險來賺取「保費」（即賣出期權所收取的權利金）並利用各種波幅衍生品來管理風險，是有可能製造出可以向投資人交代的報酬率。這其實正是當年由Scholes與Merton（BSM當中的S與M）創辦的長期資產管理公司（Long Term Capital Management, LTCM）核心套利策略的變體。用LTCM的靈魂人物黃奇輔（台灣大學校友）的話來說：

「人類社會的供給和需求有很多自然的失衡，而且失衡的兩邊都有風險，以稻米的產銷為例，個人買不到合適價格的稻米，是風險，農夫的稻米賣不出合適價格，也是風險。如果大家都不願意承擔風險的，一個潛在的需求就出現了：讓兩邊的風險降低到一個合適的程度。於是批發商應運而生，通過專業的集中收購和零售去調節失衡，降低兩邊的風險。金融風險的供需也是經常失衡。波幅衍生品的批發商就是在失衡中間提供一個服務，在金融風險供給過剩時價格會下跌，批發商買下過剩的金融風險，然後用其他金融工具把金融風險的波幅風險對沖掉，所賺的就是差價。」

每次出現重大金融危機之時，隱含方差指數都會暴升，隨後逐漸走跌回穩（如下圖）。如果這個供需再平衡的交易模式能禁得起時間考驗，確實有穩健持續發展的機會，只要記得LTCM的寶貴教訓：槓桿別拉太高。

然而在任何投資決策中，時間是最大的風險。金融市場使用數理模型與物理學與其他工程領域最大不同之處在於，未來不可預測，而且人類預測未來的嘗試隨著時間的推移變得愈來愈不準。以航太工程為例，就算將量子力學的測不準效應考慮進去，發射宇航員上天登月的計算模型仍然足夠準確。以目前的技術要推算太空船在t = 0與t = T的位置、速度等等，可以做到非常精確，但我們的數理金融模型卻不能對t = T的股價做出任何能令人有信心的推斷。目前技術能做的，僅僅是假設在市場上交易的各種金融商品的市價已經包含了對未來的預期，然後逆著時間推出一個勉強可以自圓其說的估計，用這個估計輸入用以生成該估計的公式，並用其推導出來的理論值來定價，然後再依實際交易情況修正估計。這個過程當中牽涉的變數不僅多，很多未知變數甚至不可測，而我們可能也不知道我們不知道什麼。儘管如此，「自欺欺人」的金融衍生品市場依然運作，交易仍舊蓬勃，某種意義上來說是個奇蹟。 由另一個角度來看，航海術發明於哥白尼與伽利略的時代之前，人類對海洋的探索是否因為不承認天圓地方的錯誤而被拖慢，亦是值得研究的歷史公案。

再考慮互聯網科技的飛速進展對金融市場交易的影響，完全有理由懷疑金融工程師當年建構的數理模型可能無法與時俱進。以名下管理資產超過五兆美元的貝萊德資產管理公司為例，貝萊德已經開始建構一系列完全超越傳統財務金融分析範疇的指標來更精準地掌握投資人對未來股價趨勢的判斷。以零售股為例，傳統財金分析可能是看平均單店每年、每季、每月同比與環比銷售增長，現在可能是利用衛星全球定位技術監看所有零售網點的人流，配合線上搜尋引擎關鍵字流量與信用卡消費等大數據綜合分析，直接針對經營團隊所提出的財測目標即時評價，進而設計程式買賣個股並利用金融衍生工具管理風險。這些因為技術演進所產生的新資訊與交易行為所引發的各種市場心理反應，顯然不是BSM模型的發明人在1973年所能預見的，更非所有股市參與者可以輕易理解、體會與利用。資訊不對稱造成市場不平衡，市場參與者自以為是的資訊，也有可能只是雜訊。也正因為人類不確定交易的理據是基於資訊還是雜訊，金融市場才能應運而起。這就是人性。

（貝萊德的大數據分析框架。資料來源：Blackrock）

金融大海是人性貪婪與恐懼的總和，許多人性的面向不僅難以觀測，甚至遑論預測。人類如果連對自己的人性都缺乏充分深刻的認識，又如何能期待人類發明的數理模型能夠描述、解釋與預測金融市場動向？ 如同波蘭科幻作家Stanisław Lem在經典名著《索拉力星》（Solaris）中指出的，當人類仰望包覆索拉力星的智能大海，花上幾十年努力建構理解其奧妙的複雜理論時，潛藏在大腦深處最幽微隱晦的記憶卻被索拉力星的智能大海以超時空的神秘力量萃取出來，投射到現實當中與人類互動；人類赫然驚覺，與異世界文明溝通的嘗試，只是顧影自憐的呢喃。人類其實並不真正想探索新世界，而只想在自己的世界耽溺下去，卻又無法接受其不完美。以此借鑑金融大海中互相激盪、生生不息的波紋與泡沫，

也許人類需要的不是更好的理論與模型，而是一面更澄澈的明鏡。

＊作者為旅居香港的金融觀察家與專業投資人，源鉑資本（Kyber Capital）執行長。

  （相關報導： 胡一天專欄：壟斷性行業的創新責任 ｜ 更多文章 ）