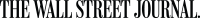金融工程的祖師爺Fisher Black(即BSM中的B)曾說:如果一個模型有缺陷,不一定是模型出問題,往往是我們對事物的認識與理解有問題。基於模型缺陷的隱含波幅微笑之所以成為金融工程產業增長的原動力,是因為很多第一代的金融工程師與在市場中實際參與交易及風險控管決策的專業人士,多半都抱持著一種迷思:如果既有的模型有缺陷,那就發明更能符合實證結果的模型。於是乎各類BSM模型的延伸紛紛出籠,用的數學愈來愈複雜,除了降低各種理工背景的火箭科學家在華爾街的失業率之外,對理解金融市場的本質不見得有幫助。直到2008年全球金融海嘯,人們才又一次學到了昂貴慘痛的教訓。監管確實變嚴格了,但各種炫技的數理模型依然持續在論文中出現,相關的新金融商品也不斷被華爾街金融化工廠合成出來向全球販賣,隱含波幅微笑曲面,依然存在。市場究竟需要新理論,還是新思維?這是一個trillion dollar question。
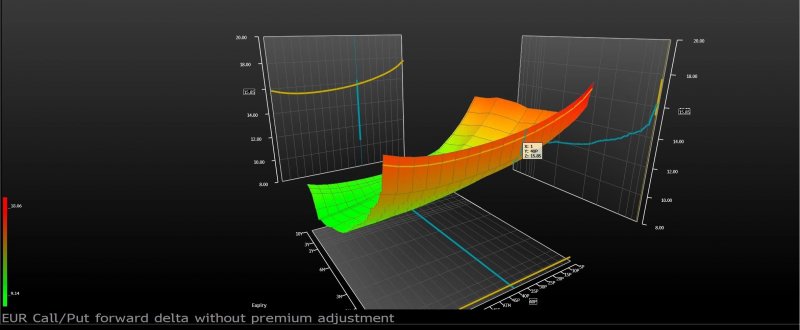
若暫時忽略金融工程本質的哲學思辨,隱含波動率微笑曲面亦提供了創造新金融商品的機會。既然隱含波幅是對未來實現的波幅的估計,華爾街就援引遠期利率是近期利率的估計這個例子,設計了一個「方差掉期互換合約」(variance swap,方差是波幅的平方,在數學上處理起來比較方便)。簡單地說,對某檔股票或股市指數未來隱含波幅看漲,可以用方差互換合約與華爾街大盤商針對未來不確定會如何浮動的隱含波幅對賭。這個賭局的累積賺賠,與前述delta hedged對沖組合相仿,可以寫成下列積分式:
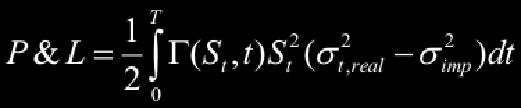
這個公式中兩種波幅的差額對股價的走勢有路徑依賴性,必須消去股價的二階影響,才能製造一個針對波幅的純粹賭局,才能更精準地對沖風險。要完全消除股價的二階影響,理論上需要一個「對數合約」-- 到期日支付股價的自然對數值的合約(因為自然對數微分兩次後會抵銷掉積分號中的股價平方項),實務上這個合約不存在,但可以用一系列歐式期權的組合來逼近對數合約的理論值。這其實正是方差互換掉期合約的風險管理核心命題,也是全球金融市場高度關注的隱含波幅指數VIX及其衍生工具的理論基礎。
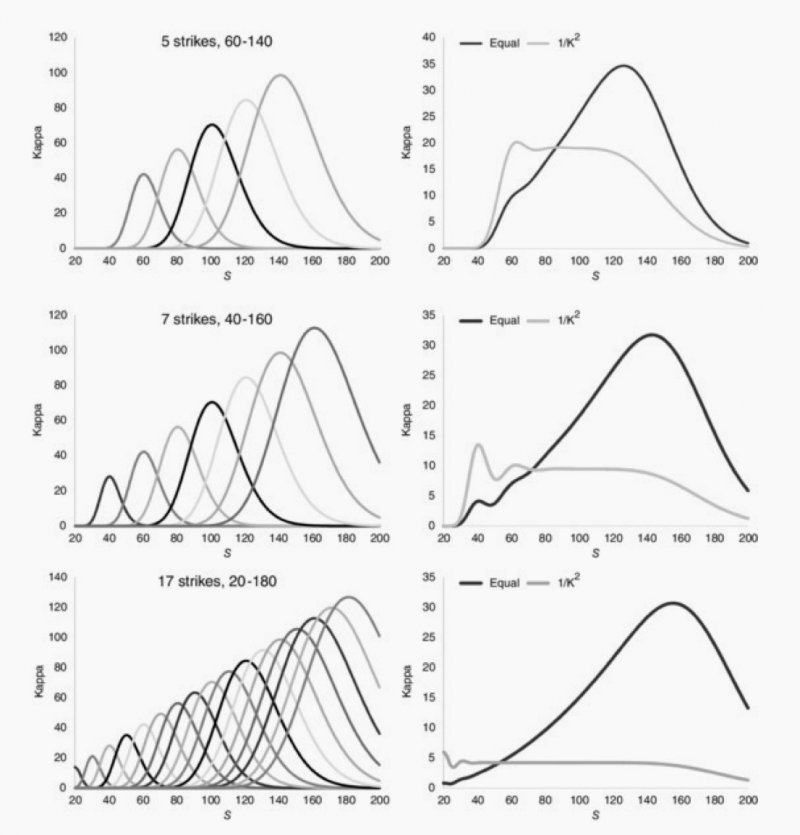
近年來許多宏觀策略對沖基金也將隱含波幅/方差的估計與風險控制列為量化交易操盤的一大重點。假設隱含波幅有一個穩定的長期平均值,且在每次偏離其平均值後都會有向該平均值回歸的趨勢,只要能夠針對這些統計特性建立禁得起壓力測試考驗的模型,無論是波段操作,或是把操盤的基金當成再保險公司,透過承擔黑天鵝風險來賺取「保費」(即賣出期權所收取的權利金)並利用各種波幅衍生品來管理風險,是有可能製造出可以向投資人交代的報酬率。這其實正是當年由Scholes與Merton(BSM當中的S與M)創辦的長期資產管理公司(Long Term Capital Management, LTCM)核心套利策略的變體。用LTCM的靈魂人物黃奇輔(台灣大學校友)的話來說: